Wordle Assistant

Web App • React.js / Entropy • 2022 - 2023

What is Wordle?

Wordle is a game that came out not so recently anymore, but gained popularity very quickly upon release. The premise of the game is to guess the secret 5-letter word of the day within 6 guesses. Each time you make a guess, the game reveals a color pattern associated with your guess that serves as a hint to help you with your next guess.

For example, if you prompt the game with

and it shows you the following pattern:

it means that the secret word has a C in the same location as your guess, an E in a location other than where it was in your guess, and no R, A, or N. Each guess reveals new information that you can use to make progress in the game. Naturally, as any statistician would, I tried to think of a way to play the game systematically.

Frequencies, right?

Opening guesses are always a topic of hot debate among players. One of my friends likes to open with the word CRANE as each letter is among the top ten most frequently appearing letters in the English language. Hitting a green on your opening guess always puts a smile on your face. Often underappreciated, is the all-gray pattern since it would actually be quite rare to find a word that doesn’t have at least one of those letters. So, are letter frequencies the key? Well, no not really.

If you can guess a word that has common letters, you can probably eliminate a fair amount of words from the resulting pattern. But consider SNAIL versus NAILS. These words have the same letters but in a different order. Just considering letter frequencies neglects this source of variation in potential answers to the puzzle.

Distribution of Patterns

So, how do we determine if one guess is better than another guess? We need some way of quantifying the notion of better. Say we guess FRAME and get the pattern below:

Of the roughly 13,000 five letter English words, only 37 match the pattern. That is a massive reduction in the answer space. But getting a pattern like this is not common. Suppose that each of the words that match—that is the 37—are equally likely to be the answer—although this isn't really the case, as some of those words would be things you would barely consider being words—then, the probability of getting this pattern is precisely ³⁷⁄_13,000. The patterns that hold a lot of information, by their very nature, are unlikely to occur. That last pattern had two greens; suppose we instead got the pattern:

Only a single yellow this time, no greens. This time the answer space may only be reduced to 2,000 possible answers, and if each was equally likely, the probability you would see this pattern is about 15%. Outcomes that are more likely are less informative.

For each word, there are 3⁵=243 possible patterns, each resulting in their reductions in the answer space. So, given a word, we can find the distribution of probabilities across the different patterns.

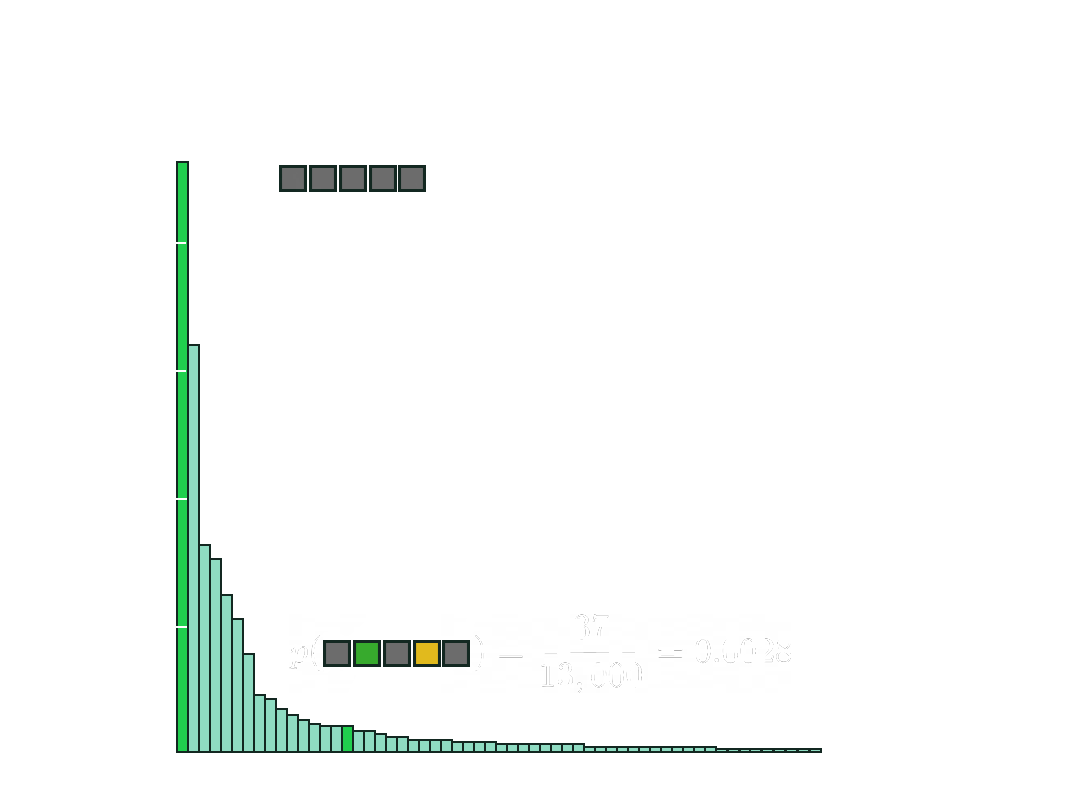
Over on the left are common patterns with large probabilities, and this long tail is where rare patterns live. When you make a guess, you hope the resulting pattern falls somewhere in this long tail.

Information Theory and Entropy

So you’ve now made your guess, and you’ve narrowed down the answer space. Say there are 10 possible words. We still haven’t really discussed how to rank them to suggest the next best guess. But we can find this pattern distribution for each one. We can judge the guesses based on the expected amount of something from each of their respective distributions. Remember that for each word, the pattern distribution is different. This is how the ordering of letters, i.e. anagrams, are accounted for. But, expectation of what? Information; cue information theory.

We say that an observation has 1 bit of information if it cuts the space of possibilities in half. If the observation cuts the space down by a factor of 4, it has 2 bits of information and so on. Mathematically,

$I = log_2(1/p )= -log_2(p)$

So now, instead of saying the probability of pattern X occurring on word Y is 0.000000004, we can say it holds 20 bits of information. For each word, based on its distribution of patterns, we can find the expected amount of information it would yield us:

$\mathbb{E}[I] = \sum_{x} p(x) \cdot log_2(1/p(x))$

Obviously, words with higher expected information are what we are looking for. We now have a metric to use as the basis of comparison. This expectation is often referred to as entropy.

Frequencies, again...

We now have a functioning assistant. During each guessing step of the game, you calculate the entropy for each word in the possible answer space and choose the one with the highest value, as it is most likely to significantly reduce the remaining possibilities. However, there is a significant oversight that becomes more apparent as you narrow down the potential answers. Let's say you have narrowed down the space to three possible words: ABBAS, LOURY, and ABYSS.

At this point, the entropy of each word will be identical since, in terms of reducing the space, they all do so by an equal amount. However, if I was playing the game instead of the assistant, I would be pretty confident that the answer were ABYSS since I have never heard of the other two. Although any five-letter word is allowed, the answers in Wordle tend to be more common words. How can we capture this preference and ensure that the assistant selects ABYSS over the others? The answer lies in relative word frequencies. Google Books provides an n-gram dataset that lists relative frequencies for every word.

So, we can simply apply the frequency as a weighting to the corresponding word, right? Problem solved. Well, not quite. Let's consider the frequency of WHICH, which is 0.00206, and compare it to the frequency of BRAID, which is 0.000002—almost 1000 times less likely. But, both of these words seem more common than ABBAS. Ideally, we need a decision boundary on the frequency list that distinguishes common words from uncommon words. By using a carefully constructed sigmoid function, we can achieve this result. The cutoff point was unfortunately chosen by eyeballing the list, but the positive aspect is that we now have a notion of the difference between a common and an uncommon word encoded as a probability. Remember how earlier we assumed that each word in the resulting answer space was equally likely to be the answer? Well, we just changed that.

The Best Opener

In this new setup, our entropies will also change. Given a word, we examine the tail of its pattern distribution. For instance, let's say we find two adjacent patterns, with the same associated probabilities as seen below.

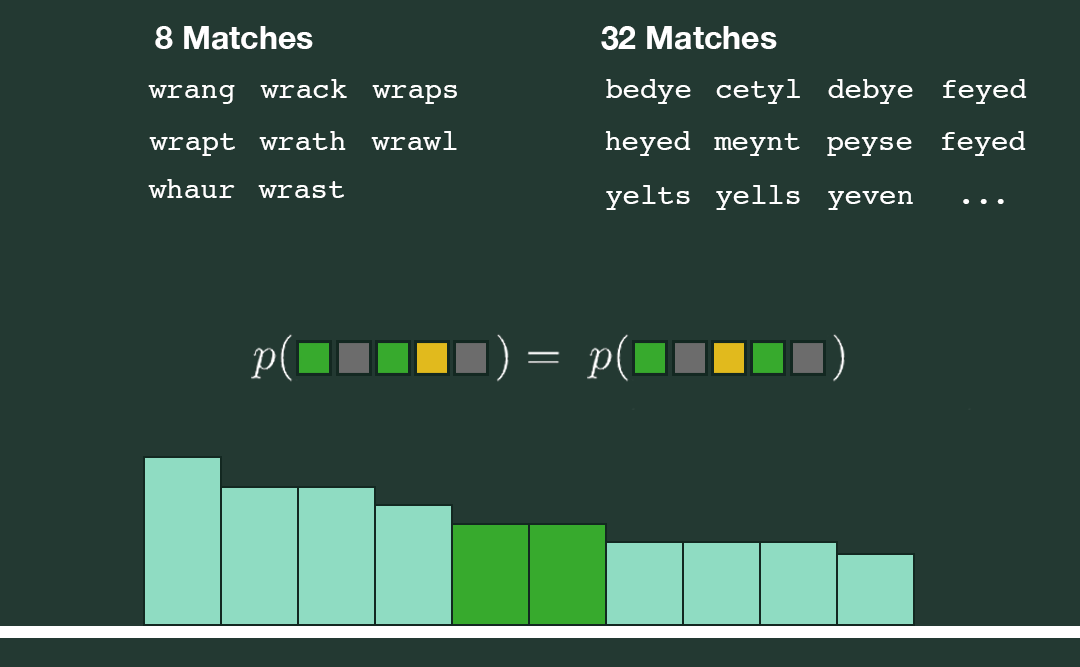
Prior to considering word frequencies, the only way these two patterns would be equally likely to appear is if the number of words in their respective reduced answer spaces were equal. However, now that we have altered the likelihood of each word being the answer, it is possible that one pattern has 8 words in its reduced answer space while the other has 32. In order for the chance of each pattern showing up to remain equal, those 8 words must be more common compared to the 32. As a result, the entropy calculation using these refined pattern distributions incorporates our preference for more common words.

Let's consider the following words:

Both DUMBO and WOMBS have higher entropies than WORMS and DORMS, but the probabilities assigned to WORMS and DORMS are larger. In the current version, the assistant considers this tradeoff by adding the two quantities, generating a score that dictates the rankings. There are other possibilities for tradeoff logic, such as using a multiplicative weight, but addition produced pretty good results.

So, what is the best opening guess? If we consider the set of all possible five-letter words and run our entropy calculations for each, we find that RATES emerges as the top choice!